CVPR2024最佳论文提名 | 神经场的网络模型正切核理论

本文是对CVPR2024最佳论文提名的工作《Grounding and Enhancing Grid-based Models for Neural Fields》的解读。该论文在盲审(pre-rebuttal)阶段获得三个审稿人的一致满分意见（5/5/5）。论文的第一作者为上海交通大学计算机系本科毕业生赵泽林（导师：人工智能学院严骏驰教授），该工作也是上海交通大学与自动驾驶企业酷哇科技的多年合作的延续成果。据悉，这是近十年中国大陆高校第一单位的首次（历史上第二次）CVPR最佳论文提名。

简述：本研究主要针对神经场提出了网格模型正切核理论。许多当代研究利用基于网格的模型来表示神经场，但对这些模型的系统分析仍然缺失，阻碍了这些模型的改进。因此，研究团队引入了一个基于网格模型的理论框架。该框架指出，这些模型的逼近和泛化行为由网格切线核（GTK）决定，GTK 是基于网格模型的内在属性，所提出的框架促进了对各种基于网格模型的一致和系统的分析。此外，该框架还激发了一个名为乘法傅里叶自适应网格（MulFAGrid）的新型基于网格模型的发展。数值分析表明，MulFAGrid 相较于其前身具有更低的泛化界限，表明其具有强大的泛化性能。实证研究表明，MulFAGrid 在包括二维图像拟合、三维符号距离场（SDF）重建和新视图合成在内的各种任务中实现了最先进的性能，展示了卓越的表示能力。研究即将在Jittor深度学习框架平台进行实现和开源。

论文链接：https://sites.google.com/view/cvpr24-2034-submission/home

神经场是基于坐标的网络，表示一个场，实质上是一种连续参数化，代表一个物体或场景的物理量。神经场应用广泛，在计算机视觉和其他研究领域的各种任务中显示出了显著的成功。

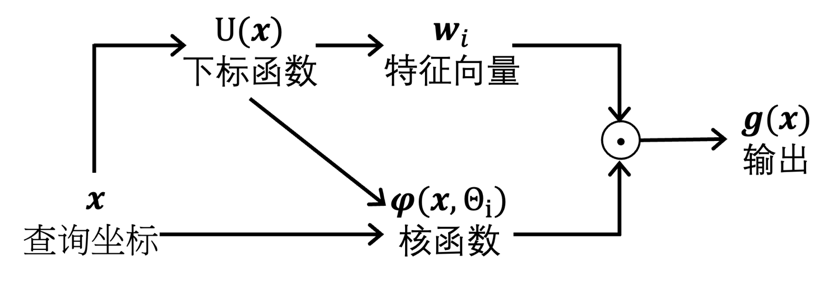
该研究主要针对网格模型（grid-based models），这是一类主要的神经场模型。网格模型在参数化和功能上与传统的神经网络（如MLP）有根本不同。主要的不同包括MLP往往包含多层非线性神经网络，不显示查询的过程，同时MLP的输入也不一定要求位置坐标。如下图所示，网格模型以查询坐标为输入，该坐标被发送到下标函数，以从网格中获取一组特征向量。然后，模型输出核函数和这些特征向量的加权平均值。该模型需要学习参数的主要是特征向量。最简单的核函数是不含参数的插值算法（如最近邻算法或者双线性插值算法），核函数里也可以包含可学习的参数。

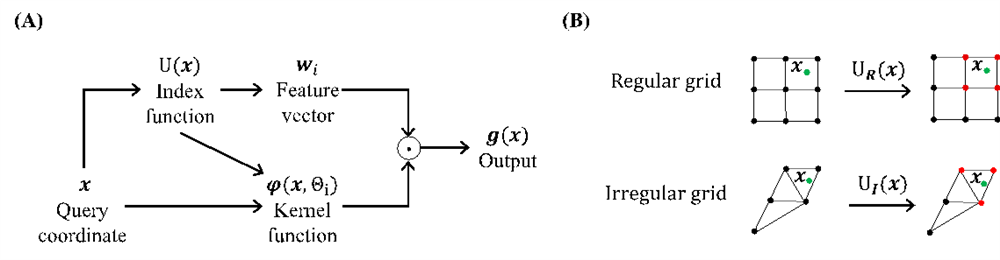
下图中（A）是英文版的网格模型的示意图，（B）表明选择下标函数的不同可以让研究提出的算法适配不同的网格模型。之前的NeRF方法DVGO使用了规则的网格，而目前比较火热的3DGS则是采用了非规则网格（点云）。

该研究的理论旨在通过三个主要问题来理解和增强网格模型：

（1）我们如何理解网格模型的训练动态？

（2）我们如何衡量网格模型的泛化性能？

（3）我们如何设计一个更好的网格模型？

为了解决这些问题，研究提出了一个基于正切核（tangent kernels）的理论框架。

这里先介绍什么是正切核。正切核这一概念来自于著名的深度学习理论文章神经正切核（Neural Tangent Kernels，NTK）。NTK 是一种核函数，最初由研究者在研究神经网络的训练过程时提出。当神经网络在参数空间中靠近其初始值时，通过对神经网络梯度下降优化过程的分析，发现网络的行为可以用一个固定的核函数来描述，这个核函数就是神经正切核。比如神经网络的输出可以用其参数的梯度来表示。在训练过程中，网络参数的更新会导致输出的变化，而这种变化在参数空间中的变化速率可以用梯度来表示。NTK 定义了两个输入数据点的输出变化之间的相似度。形式上，对于输入数据点  和，神经正切核可以定义为网络输出对参数的梯度的内积：

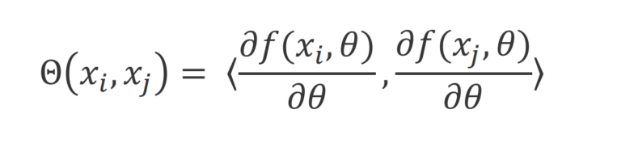
其中，是神经网络的输出，是网络的参数。

研究的理论结果表明，网格模型的近似和泛化性能与网格切线核（GTK）有关。GTK被定义为一个正半定矩阵，它测量梯度空间中两个数据点之间的距离。论文展示了GTK的定义：g是由w(t)参数化的网格模型，X是一个数据集，其中Xi是第i个数据。GTK可以这样表示：

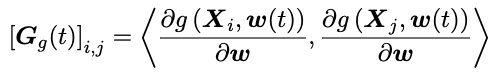
这一形式跟神经正切核（NTK）的形式是吻合的，作为正切核，它们的主要区别是适用的模型不同，GTK主要适用于网格模型。网格模型本质上比较简单纯粹，所以GTK的理论基本不需要近似，但是NTK的理论需要网络无穷宽的假设才能成立。

-定理1：网格模型优化定理

定理一（网格模型优化定理）说明，网格模型的模型参数根据微分方程（如:方程所示）演化。

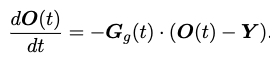
这里O(t)表示网格模型的输出，G(t)表示网格模型的GTK，而这里的Y表示数据集的标签（向量化，Yi表示第i个数据的标签），对该定理进行简单证明，模型的参数在梯度下降算法下按照下面的公式进行迭代：

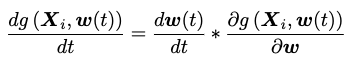
此时考虑一个L2损失函数L，它的梯度将被运用于更新模型参数：

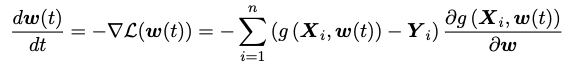
结合以上两个方程，可以得到：

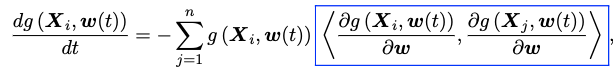
蓝色方框里即研究关注的GTK。该定理的意义在于可以预测模型的效果（不用亲自“炼丹”即可确定模型的好坏），因此其在理论上有很高的价值，也是朴素成立的，不依赖于具体的模型细节。对定理1进行总结：

-定理2：GTK不变定理

接下来，研究提出了另一个定理（GTK不变定理）。定理2指出，网格模型的GTK在训练期间保持不变。这意味着无论网格模型的大小如何，初始GTK在整个训练过程中保持恒定。这一定理揭示了GTK是由模型和数据集决定的内在特性，与模型的训练过程无关，有了这个定理，自然也不难理解网格模型的很多性质都与GTK有关了。对定理2进行总结：

-定理3：网络模型的泛化性

定理3可以描述网格模型的泛化性能。在理论深度学习中，泛化性能的好坏通常由泛化界（generalization bound）来刻画。该定理揭示了网格模型的泛化界由一个特定的度量决定，而，与网格模型的GTK和数据集的标注有关。该泛化界提供了模型性能的概率保证。定理3说明了模型的泛化性能既与GTK有关，也与数据集的结构有关。结合该定理与GTK的特征值，能够获得更多关于泛化性能的信息。在论文的补充材料中可以找到对定理的证明。对定理3进行总结：

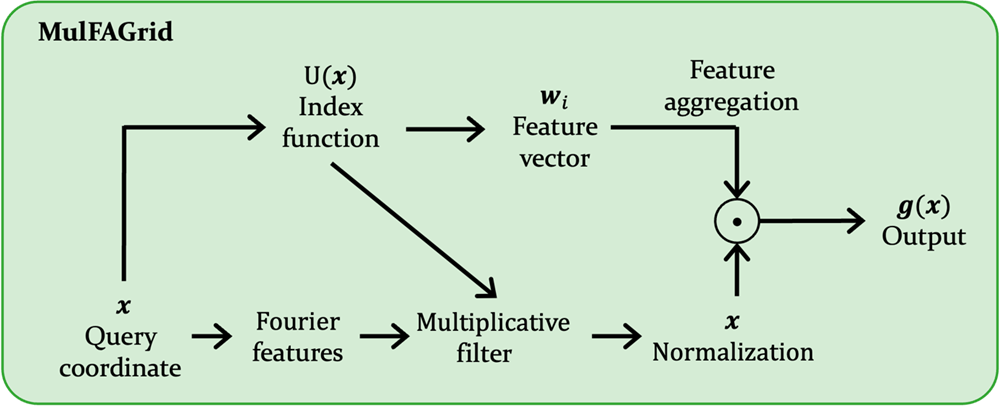
GTK理论可以激发未来设计具有更好训练和泛化性能的网格模型。研究团队介绍了一种新的网格模型，名为MulFAGrid。该模型使用傅里叶特征来提升高频信号的学习，并采用乘法滤波器来为模型提供节点信息。模型的示意图如下：

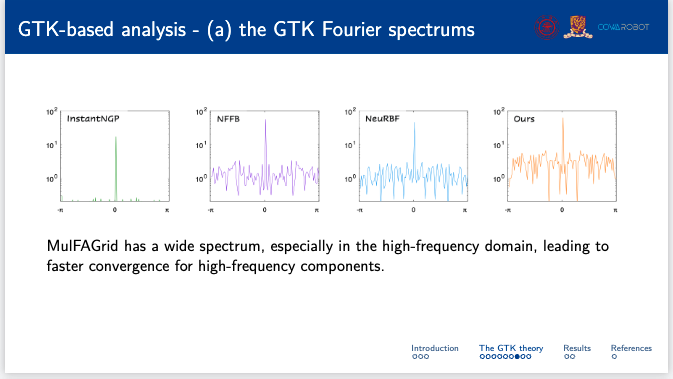
研究团队基于GTK理论展示了一组数值实验。首先，在频谱分析中，MulFAGrid显示了比较宽的频谱，特别是在高频域。这一特性导致高频成分的收敛速度更快。

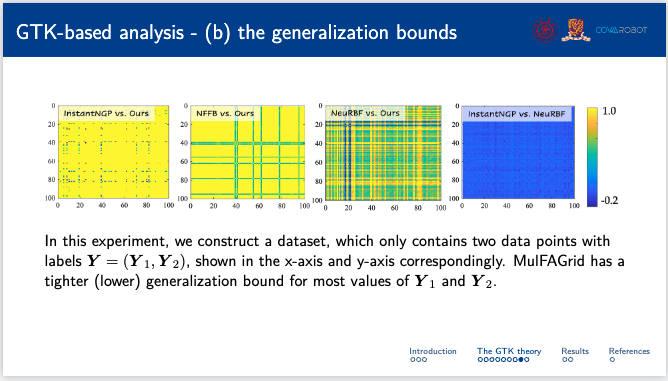
在该实验中，研究团队构建了一个包含两个数据点及其对应标签的数据集。MulFAGrid对于大多数标签值表现出更紧的泛化界，表明其性能更好。

下图展示了各种基线方法和研究的误差图，其中误差图用于衡量预测图像与真实图像的差异。MulFAGrid提供了更准确的拟合，展示了其优越的性能。

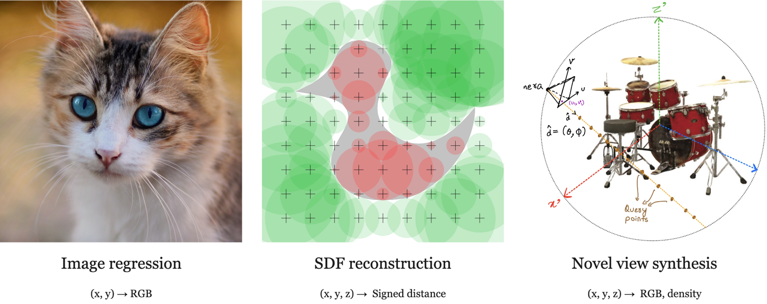
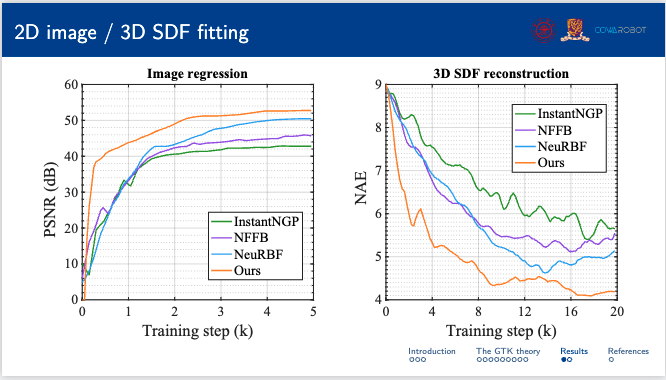
下图展示了模型在拟合二维图像和三维符号距离函数（SDF）方面的性能，结果突出了MulFAGrid的准确性和效率。

最后，研究团队展示了在新视角合成方面的结果。详细结果表明，MulFAGrid在生成高质量的新视角方面表现出色，突显了其实际应用性。

了解更多详细内容，请关注该论文（Jittor版本）的Project Page，点击阅读原文可达。